Counting Inversions: A Comprehensive Guide

What is an Inversion?

An inversion in an array is a pair of indices (i, j) such that i < j and arr[i] > arr[j]. Counting the number of inversions helps understand the disorder of an array.

Importance of Counting Inversions

1. Measure of Sorting: The number of inversions indicates how far an array is from being sorted.
2. Performance Metrics: Inversions are useful in assessing sorting algorithms and their efficiencies.

Basic Approaches to Count Inversions

1. Brute Force Approach

• Time Complexity: O(n^2)
• Method: Use two nested loops to count inversions by comparing all pairs.
• Code Example:

def count_inversions_brute_force(arr):
    count = 0
    n = len(arr)
    for i in range(n):
        for j in range(i + 1, n):
            if arr[i] > arr[j]:
                count += 1
    return count

2. Merge Sort Approach

• Time Complexity: O(n log n)
• Method: Leverage the merge sort algorithm to count inversions while merging.
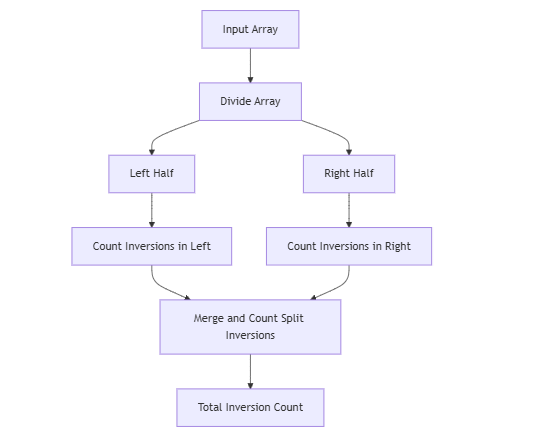
• Key Steps:
  1. Divide the array into two halves.
  2. Recursively count inversions in each half.
  3. Count inversions while merging the two halves.
  4. Add the counts to get the total number of inversions.

Understanding the Merge Sort Approach

Merge Function

While merging two sorted subarrays:

• For each element in the left subarray, count how many elements in the right subarray are smaller.
• This is done using the formula mid - i + 1 when arr[i] > arr[j].

Recursive Counting Function

Recursively split the array until single elements remain, and then merge while counting inversions.

Code Example

def merge_and_count(arr, temp_arr, left, mid, right):
    i = left    # Starting index for left subarray
    j = mid + 1 # Starting index for right subarray
    k = left    # Starting index for sorted array
    inv_count = 0

    while i <= mid and j <= right:
        if arr[i] <= arr[j]:
            temp_arr[k] = arr[i]
            i += 1
        else:
            temp_arr[k] = arr[j]
            inv_count += (mid - i + 1) # Count inversions
            j += 1
        k += 1
    
    while i <= mid:  # Copy remaining elements of left subarray
        temp_arr[k] = arr[i]
        i += 1
        k += 1
    
    while j <= right:  # Copy remaining elements of right subarray
        temp_arr[k] = arr[j]
        j += 1
        k += 1
    
    for i in range(left, right + 1):  # Copy sorted subarray to original
        arr[i] = temp_arr[i]

    return inv_count

def merge_sort_and_count(arr, temp_arr, left, right):
    inv_count = 0
    if left < right:
        mid = (left + right) // 2
        inv_count += merge_sort_and_count(arr, temp_arr, left, mid)
        inv_count += merge_sort_and_count(arr, temp_arr, mid + 1, right)
        inv_count += merge_and_count(arr, temp_arr, left, mid, right)
    return inv_count

def count_inversions(arr):
    temp_arr = [0] * len(arr)
    return merge_sort_and_count(arr, temp_arr, 0, len(arr) - 1)

Key Concepts to Focus On

1. Sorting Algorithms: Understanding merge sort is crucial since inversion counting leverages it.
2. Divide and Conquer: Grasping the divide and conquer approach helps in numerous algorithms, not just inversion counting.
3. Recursion: Practice writing recursive functions and comprehending their base cases and recursive cases.
4. Complexity Analysis: Learn to analyze the time and space complexity of your algorithms.
5. Edge Cases: Consider arrays with different characteristics (e.g., already sorted, reverse sorted, duplicates) and how your algorithm handles them.

Practice Problems

• Count inversions in various arrays.
• Modify the inversion counting algorithm to count other metrics (e.g., pairs with a certain condition).
• Implement similar counting problems using different sorting algorithms.

Conclusion

Counting inversions is a classic problem that illustrates the power of efficient algorithms. Mastering this topic builds a solid foundation for understanding more complex data structures and algorithms. Regular practice and engagement with related problems will reinforce these concepts.

Process Diagram